Trên diễn đàn đã có nhiều bài viết về nguyên lí vật lí trong judo cũng như trong Aikido. Tuy nhiên mình thấy có 1 số điểm quan trọng mà các bài này chưa nhắc đến. Mới đây mình được biết đến cuốn sách Scientific Basis of Human Motion, mô tả về nguyên lí vật lí trong các chuyển động của con người. Sách k có bản mềm, mình chỉ tìm được slide bài giảng của vài chương trong sách, nhưng đọc thấy rất thú vị. Dựa vào các bài giảng này, mình lọc ra 1 số kiến thức cơ bản nhất để giới thiệu đến mọi người. Mình cố lấy ví dụ cho gần gũi với việc luyện tập, không đi quá sâu vào chi tiết vật lí để anh em dễ hiểu hơn. Nếu sai sót gì mong mọi người cứ góp ý thoải mái nhé!
I. Vài điều cơ bản về lực và chuyển động
Lực có thể kể đến lực tự nhiên (trọng lực, lực ma sát,…) và lực nhân tạo (lực do cơ vân tạo ra)
3 định luật Newton về lực
1. Vật sẽ giữ nguyên trạng thái chuyển động với vận tốc không đổi trừ khi bị tác động của lực từ bên ngoài.
Nghĩa là vật nào cũng có quán tính. Ví dụ như cái xe mất phanh sẽ tiếp tục di chuyển cho đến lúc bị tác động lực cản (bởi gốc cây chẳng hạn).
2. Độ lớn của gia tốc (a) tỉ lệ thuận với lực (F) và tỉ lệ nghịch với vận tốc (v) của vật. Công thức là F=m.a
Hiều đơn giản là nắm đấm càng nặng, và ra đòn càng nhanh thì lực của cú đấm vào mặt đối thủ sẽ càng lớn.
3. Lực tác dụng bằng lực phản tác dụng.
Ví dụ khi tác động lực bằng nắm đấm vào mặt đối thủ thì mặt đối thủ cũng sẽ tác động lại nắm đấm của mình 1 lực như vậy. Đấy là lí do đấm người khác càng mạnh thì tay càng đau. Lưu ý: 2 lực này cùng độ lớn, cũng phương, ngược chiều nhưng không phải 2 lực cân bằng do điểm đặt khác nhau: lực của ta đặt vào mặt đối thủ, còn lực của đối thủ đặt vào nắm đấm của ta. Thế nên trong các đòn đánh thường dùng bộ phận khó bị tổn thương của mình để đánh vào chỗ dễ tổn thương của địch, chứ k ai dùng mũi để đả thương nắm tay của đối thủ bao giờ.
II. Chuyển động
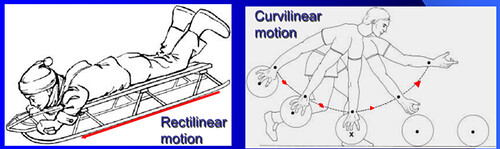
Chuyển động có tịnh tiến (tuyến tính và phi tuyến tính) và chuyển động quay quanh trục.
Nếu phương của lực tác động không đi qua trọng tâm thì vật chuyển động quay. Trọng tâm là gì ta sẽ bàn đến sau. Lấy ví dụ trong đòn Kaiten nage, bước ném cuối cùng. Nếu muốn Uke ngã lăn tròn, thì tác động lực vào tay và giữ cổ uke như hình dưới. Nếu để tay uke kẹp sát vào sườn và đẩy thẳng vào trọng tâm thì sẽ khiến uke chúi vế phía trước chứ khó lăn (tịnh tiến) (Gần như kiểu đánh kaiten nage ở phút 0:23 trong clip dưới)
III. Trọng tâm
1. Trọn tâm là điểm đặt của trọng lực, là nơi tất cả các lực tác động lên cơ thể được tổng hợp lại. Khi cơ thể thay đổi vị trí thì trọng tâm cũng thay đổi theo
Vị trí của trọng tâm tùy thuộc vào hình dáng cơ thể. Thông thường trọng tâm của nữ năm ở độ cao khoảng 55% chiều cao cơ thể, ở nam là khoảng 57%.
• Ổn định và cân bằng
Tất cả các vật cân bằng ở trạng thái nghỉ, khi đó tổng các lực tác động lên vật bằng 0, tức là các lực cân bằng nhau. Cân bằng cũng có 2 loại là cân bằng bền (ổn định) và cân bằng không bền (không ổn định)
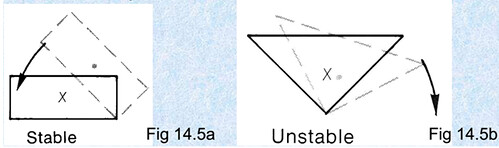
Cân bằng bền là trọng tâm ở vị trí thấp nhất so với các vị trí lân cận của nó.
Cân bằng không bền là khi trọng tâm ở vị trí cao nhất so với các vị trí lân cận của nó. Khi vật ở trạng thái cân bằng không bền thì chỉ cần 1 lực nhỏ cũng có thể đưa vật ra khỏi vị trí cân bằng (thông thường là trọng tâm của nó sẽ về vị trí thấp hơn) và không thể tự trở về vị trí cũ. Cân bằng bền thì ngược lại.
Ví dụ như viên bi trong hình 20.2 phía dưới, vị trí A là vị trí cân bằng bền, nếu đưa nó lên vị trí B rồi thả tay, nó sẽ tự lăn về vị trí A
Nói nôm na là trọng tâm càng ở thấp thì càng bền
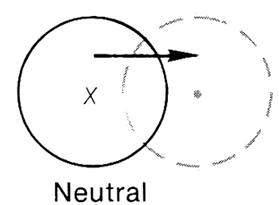
Ngoài ra còn có cân bằng phiếm định: Khi trọng tâm không thay đổi vị trí (cao hơn hoặc thấp hơn). Ví dụ trọng tâm của quá bóng luôn là tâm hình cầu, dù lăn thế nào thì trọng tâm đó cũng không đổi độ cao và nó có thể cân bằng ở mọi vị trí lăn (tất nhiên là xét trên mặt phẳng)
VD về cân bằng phiếm định: Trọng tâm của đô vật bên trái hầu như k thay đổi độ cao
Các hướng đẩy làm uke MTB: đẩy trọng tâm ra khỏi chân đế
Khi bị tác động rời khỏi trạng thái cân bằng, con người luôn có phản xạ lấy lại thăng bằng. VD: khi bị đẩy thì lùi chân lại, ngã thì đưa tay chống.
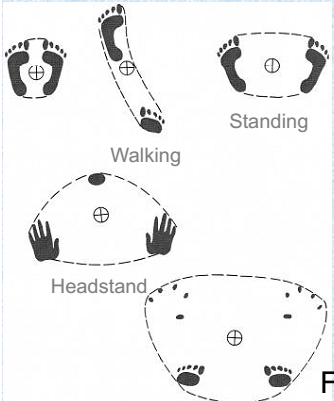
2. Một vật cân bằng (thăng bằng) khi hình chiếu của trọng tâm lên mặt đất nằm trong diện tích mặt chân đế. Mặt chân đế càng rộng thì càng dễ giữ thăng bằng. Hình dưới biểu diễn vị trí hình chiếu của trọng tâm với chân đế trong 1 số vị trí thăng bằng
Trọng tâm có thể thay đổi vị trí theo các tư thế. Trọng tâm càng gần chân đế thì trạng thái thăng bằng càng ổn định.
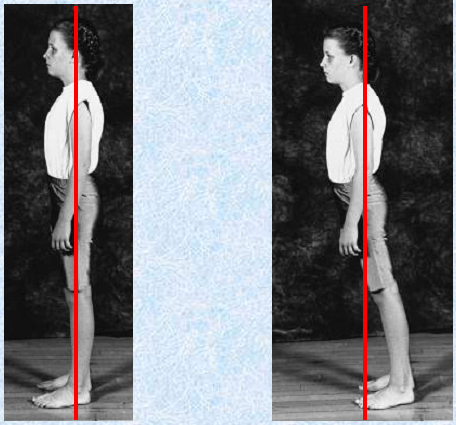
Cơ thể gồm nhiều bồ phận. Khi đứng ở tư thế tự nhiên, thả lỏng, các bộ phân sẽ nằm trên cùng 1 đường thẳng vuông góc mặt đất đi qua trọng tâm, khi đó có thể đạt trạng thái cân bằng mà không cần nhiều sức. Khi các bộ phận cơ thể lệch khỏi đường thẳng này thì sẽ phải dùng thêm sức để giữ thăng bằng.
VD phía dưới, nếu đứng lệch như hình bên phải thì phải dùng nhiều cơ bắp để giữ thăng bằng hơn.
Đó cũng là lí do trong thế thủ phải giữ thẳng trục chính tâm
Chuyển động và cân bằng là 2 trạng thái đối lập. Điểm tới hạn là điểm mà tại đó vật chuyển từ trạng thái chuyển động sang trạng thái cân bằng hoặc ngược lại
IV. Ứng dụng trong Aikido
Khi đã biết nguyên lí của trạng thái thăng bằng, ta có thể hiểu được cách làm mất thăng bằng cơ bản là đưa trọng tâm của đối phương di chuyển ra khỏi chân đế. Tất nhiên sẽ có khó khăn vì uke luôn có phản xạ lấy lại thăng bằng, cụ thể là thay đổi chân đế để đỡ lấy trọng tâm (bước chân, chống tay xuống đất,..). Muốn uke ngã thì phải hạn chế việc di chuyển chân đế của uke. Rõ nhất là trong judo, các đòn chân Ashi waza. Trong Aikido thì không có ngáng chân nên mỗi đòn phải có cách riêng. Cụ thể hơn, mọi người có thể tham khảo ở loạt bài "Mất thăng bằng" trong box kĩ thuật của 4rum









 Trả lời kèm Trích dẫn
Trả lời kèm Trích dẫn


 . Cảm ơn các bác nhiều.
. Cảm ơn các bác nhiều.
